 同人誌即売会では、ブースに来て頂いた方がクルタ計算機を好きに触れるように展示しています。その際、ほとんどの方が引き算を試みようとして、ハンドルを逆回しにしようとします(そして回せずにアレ?と思われます)。
同人誌即売会では、ブースに来て頂いた方がクルタ計算機を好きに触れるように展示しています。その際、ほとんどの方が引き算を試みようとして、ハンドルを逆回しにしようとします(そして回せずにアレ?と思われます)。
足し算と引き算について、ハンドルの回転方向と関係があってしかるべきというのは、設計者のクルト・ヘルツシュタルク氏も念頭にあったようです。彼はこの引き算実装についてかなり悩んでいたようです。
引き算はまだできなかった。というのも逆方向に操作して元に戻そうとすると、繰り下げ時に繰り下げるべき桁が計算位置を既に過ぎているからだ。
クルト・ヘルツシュタルク(訳:gotcha)
この後、クルトは「補数を加算すれば、引き算と同じ結果が得られる」と思いつき、クルタ計算機に引き算機能を実装します。
この “補数を” 加算という話が、どうもピンとこないという話を聞き受けましたので、今回のエントリで説明します。
10進数の補数とは
補数という言葉については、いくつか説明方法があります。私のように、コンピュータにおける情報処理から補数に触れた人は、2進数の補数についてよく覚えていることでしょう。いちおう、補数という言葉の定義としては
負の数を表現する一つの手法で,r 進数 n 桁の数を扱っている場合,ある数 x の補数は rn−x で表わす。(中略)十進法で9の補数という表示の仕方もある。これは数値の各桁ごとに10の補数をとるもので,38の9の補数は 61である。9の補数に1を加えたものが10の補数となる。数の引き算は補数の加算で行うことができる。
ブリタニカ国際大百科事典(10進数に限った説明に要約している)
との説明もありますが、私のように数学が苦手な方はここらへんで肛門が痒くなってくると思います。
各桁の「9の補数」をまず対応表で求め、1を加えて、10の補数にする。
「10の補数」というのが、クルトやブリタニカが言う「補数」のことです。10進数だから、10の補数と呼ぶわけですね。それを求めるには、1桁の数値でまず9の補数を求めていくやりかたが簡単です。ブリタニカが示した公式で求めれば、「“8”の9の補数」は1となります。一覧表にすると、こうなります。
| 元の数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 9の補数 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
たとえば、360 という3桁の数値を、補数(10進数の補数、つまり「10の補数」)に変換してみましょう。
まず、一覧表で各桁を9の補数にします。
360 → 639
この 639 に1を加えたら、10の補数「640」となります。
クルタ計算機で試してみましょう
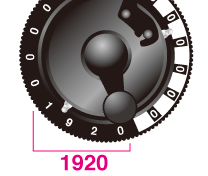
クルタ計算機 Type1 のイラストを使って、実際の引き算を再現してみましょう。
- 1920 – 360 = 1560
まず、すでに計算結果ダイヤルに 1920 という数値が既にあるとします。Type1 は11桁なので、右図のように 00000001920 と表示されています。
置数ノブの数値を、補数に変換する
 次に置数ノブで360を入力します。置数ノブは8桁なので、00000360 となっています。ハンドルを引き上げてマイナスモードにしましょう。ハンドルを引き上げたことで、内部の段付き歯車が、置数ノブの各桁を9の補数に変換します。
次に置数ノブで360を入力します。置数ノブは8桁なので、00000360 となっています。ハンドルを引き上げてマイナスモードにしましょう。ハンドルを引き上げたことで、内部の段付き歯車が、置数ノブの各桁を9の補数に変換します。
TYPE1は11桁の計算機なので、 00000000360 は11桁(左側の0も含みます)の数字として扱われ、各桁の9の補数は
99999999639
となります。これに1を加算すると 、10の補数「99999999640」になるわけです。この数値が、10進数の360の補数です。
そして演算を実行してみまましょう
ユーザーがハンドルを回して演算を行うと
00000001920 + 99999999639 + 1 = 100,000,001,560
という計算が実行されます。最後に1を足すことで、9の補数を10の補数にしています。計算結果は12桁の数値ですが、計算結果ダイヤルは11桁しかないので、12桁目の1は桁があふれて表示されません。
| ダイヤルの1920 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 9 | 2 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10の補数に変換した360 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 6 | 4 | 0 | |
| 加算結果 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 5 | 6 | 0 |
これより、1920 – 360 = 1560 という引き算が実現しているのです。



この記事へのコメントはありません。